您當前位置:首頁 > 知產百科 > 文章正文
內插法是什么意思(內插法的原理)
內插法是什么意思?
內插法,又叫插值法。內插法,一般是指數學上的直線內插,利用等比關系,是用一組已知的未知函數的自變量的值和與它對應的函數值來求一種求未知函數其它值的近似計算方法,是一種未知函數,數值內插法逼近求法。
在內含報酬率中的計算
內插法在內含報酬率的計算中應用較多。內含報酬率是使投資項目的凈現值等于零時的折現率,通過內含報酬率的計算,可以判斷該項目是否可行,如果計算出來的內含報酬率高于必要報酬率,內插法則方案可行;如果計算出來的內含報酬率小于必要報酬率,則方案不可行。一般情況下,內含報酬率的計算都會涉及到內插法的計算。不過一般要分成這樣兩種情況:
1.如果某一個投資項目是在投資起點一次投入,經營期內各年現金流量相等,而且是后付年金的情況下,可以先按照年金法確定出內含報酬率的估計值范圍,再利用內插法確定內含報酬率;
2.如果上述條件不能同時滿足,就不能按照上述方法直接求出,而是要通過多次試誤求出內含報酬率的估值范圍,再采用內插法確定內含報酬率。
內含報酬率(IRR)插值法計算方法
適用條件:全部投資在0時點一次投入,投產后至項目終結時,各年現金凈流量符合普通年金形式,:
由NPV=NCF×(P/A,IRR,n)-C=0,可推出:
(P/A,IRR,n)=C/NCF
即:已知現值(原始投資額現值C)、年金(投產后每年的凈現金流量NCF)、期數(項目壽命期n),求利率IRR。
【注意】IRR所對應的年金現值系數在數值上等于該項目的靜態回收期。
內插法的原理:
內插法的原理是根據比例關系建立一個方程,然后,解方程計算得出所要求的數據。
例如:假設與A1對應的數據是B1,與A2對應的數據是B2,現在已知與A對應的數據是B,A介于A1和A2之間,則可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)計算得出A的數值,其中A1、A2、B1、B2、B都是已知數據。

推薦閱讀:
.jpg)
.png)

最新文章
 稅務登記證可以注銷嗎(稅務注銷需要什么材料和流程)
稅務登記證可以注銷嗎(稅務注銷需要什么材料和流程)
 注冊一個公司的流程怎樣費用多少(注冊公司的手續和費用標準)
注冊一個公司的流程怎樣費用多少(注冊公司的手續和費用標準)
 辦理股東變更需要什么資料(股份變更流程)
辦理股東變更需要什么資料(股份變更流程)
 寧波注冊公司流程及費用(寧波注冊公司的完整流程)
寧波注冊公司流程及費用(寧波注冊公司的完整流程)
 辦理分公司需要帶什么資料(注冊分公司的流程和所需材料)
辦理分公司需要帶什么資料(注冊分公司的流程和所需材料)
熱門文章
如何查詢中小企業名單(中小微企業名錄查詢系統入口)5663人閱讀
 國家企業信用公示信息系統山西入口(企業信息公示年報流程)
國家企業信用公示信息系統山西入口(企業信息公示年報流程) 3916人閱讀
 如何查詢商標注冊情況(注冊商標名稱查詢詳細步驟)
如何查詢商標注冊情況(注冊商標名稱查詢詳細步驟) 2542人閱讀
 廣州紅盾網企業信息查詢系統入口(紅盾網企業信息查詢流程)
廣州紅盾網企業信息查詢系統入口(紅盾網企業信息查詢流程) 1980人閱讀
 國家企業信用公示信息系統湖北入口(工商年報公示流程)
國家企業信用公示信息系統湖北入口(工商年報公示流程) 1662人閱讀
 內蒙古企業信用信息查詢公示系統入口(企業公示年報流程)
內蒙古企業信用信息查詢公示系統入口(企業公示年報流程) 1555人閱讀
 遼寧省企業信用公示信息系統入口(工商年檢具體操作步驟)
遼寧省企業信用公示信息系統入口(工商年檢具體操作步驟) 1414人閱讀
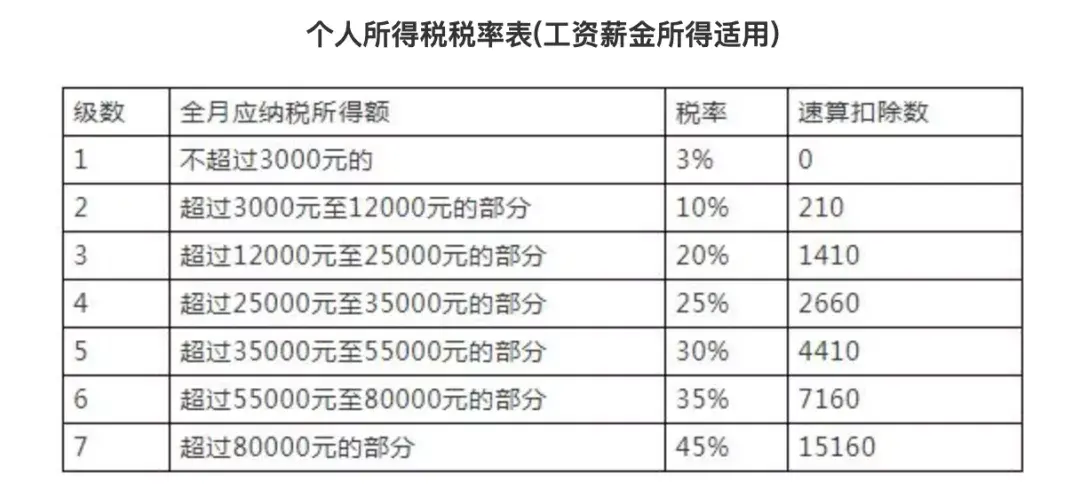
 員工工資超過5000怎么扣稅(5000以上扣稅標準稅率表)
員工工資超過5000怎么扣稅(5000以上扣稅標準稅率表) 1393人閱讀
 食品經營許可證網上申請登錄入口(山東食品經營許可備案系統操作流程)
食品經營許可證網上申請登錄入口(山東食品經營許可備案系統操作流程) 1207人閱讀
 國家企業信用公示信息系統四川入口(企業信用信息公示填報流程)
國家企業信用公示信息系統四川入口(企業信用信息公示填報流程) 1146人閱讀






.png)
.png)
.png)




